Abstract: This paper presents a piecewise nonlinear approximation algorithm for calculating transcendental functions, with a focus on the Sigmoid function, which is widely used in neural networks. A segmentation strategy is introduced based on the symmetry of the function and the non-uniformity of its derivative. The impact of the proposed method and the order of the approximating polynomial on the accuracy of the results is analyzed. The algorithm is implemented on an FPGA, and a third-order polynomial is used to process the Sigmoid function. The design achieves a precision of up to 10-5 and a maximum frequency of 127.327 MHz, meeting the requirements for high-speed and high-precision computation.

In fields such as real-time image processing and digital signal processing, high-speed computation of nonlinear functions is often required [1]. In artificial neural networks, a large number of nonlinear functions must be calculated. Therefore, it is of great importance to study how to perform fast processing of nonlinear functions in this domain. Among these, the Sigmoid function is the most commonly used. Current research on Sigmoid function implementation is mainly divided into software and hardware approaches. Software implementations are generally slower and less parallel, making them unsuitable for high-speed processing [2]. With the rapid development of very large scale integrated circuits, it has become increasingly important to explore efficient hardware-based methods for computing Sigmoid functions.
FPGAs, with their reconfigurable nature, offer a powerful solution for high-speed computation involving Sigmoid functions. Common methods for implementing Sigmoid functions on FPGAs include lookup tables, CORDIC algorithms, Taylor series expansion, and piecewise linear approximation. While lookup tables are easy to implement, they require significant memory resources as accuracy and interval size increase. The CORDIC algorithm relies on multiple iterations, which can slow down performance as precision improves. The Taylor series approach demands many multipliers and adders, leading to high resource consumption. Piecewise linear approximation, however, combines lookup tables with low-order polynomials, offering faster computation and is currently the mainstream approach. However, its accuracy is limited due to the use of low-order polynomials over small intervals.
To address these challenges, this paper applies a traditional piecewise nonlinear approximation method to the Sigmoid function. Previous work [8] used similar techniques for hyperbolic tangent functions, but lacked a clear basis for segmentation and showed inconsistent accuracy across segments. To improve this, we take the Sigmoid function as our focus, leveraging its symmetry and derivative characteristics. We apply the least squares method from numerical analysis to develop a reasonable segmentation strategy. We also compare the accuracy differences between uniform and adaptive segmentation methods. A hardware architecture is designed using a hardware description language and tested on a Xilinx Virtex-5 XC5VLX110T device. The design is evaluated in terms of resource usage, speed, and accuracy.
1 Piecewise Nonlinear Fitting Scheme and Result Analysis of Sigmoid FunctionThe basic principle of piecewise nonlinear approximation involves dividing the function into segments and approximating each segment with a higher-order polynomial. This transforms the complex computation of a nonlinear function into a simpler polynomial calculation task.
According to Taylor's formula, the function is expanded around a certain point. As more terms are included, the approximation error decreases. However, the value of the (N+1)-th derivative directly influences the accuracy of the N-th order polynomial approximation. If the absolute value of the derivative is large, the error increases, requiring smaller intervals. Conversely, if the derivative is small, larger intervals can be used. By dynamically adjusting the segmentation based on the derivative values, the approximation can be optimized to reduce errors.
We analyze the properties of the Sigmoid function and its fourth derivative, as shown in Figure 1. When sufficient segmentation is ensured, a third-order polynomial can achieve high accuracy. Here are some key observations:
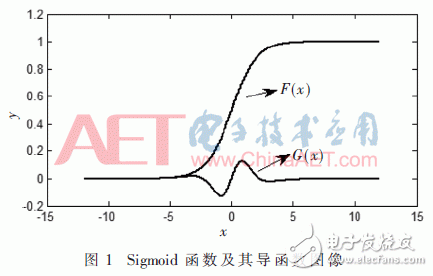
(1) The Sigmoid function is symmetric about the point (0, 0.5). This allows us to compute only one half of the function and derive the other half through symmetry.
(2) For the positive interval, the fourth derivative reaches its maximum near x = 1 and gradually decreases toward both ends. As x increases, the fourth derivative tends to zero.
Fume EXTRA is a pre-filled Disposable Vape pen that lasts 5 times longer than traditional 300-puff e-cigarette devices. The plus-size disposable vaping kit generates 1500 hits of 5% strength salt nicotine flavor. Each one-use vaporizer is powered by a built-in 850mAh battery and pre-loaded with 6ml of vape juice. Enjoy EXTRA hits without breaking your wallet. Shop All 24 Fume flavors today.
Fume Ultra.Fume Ultra 2500puffs.Fume Ultra disposable vape,Fume Ultra vape,fume vape.
Shenzhen Ousida Technology Co., Ltd , https://en.osdvape.com